2.1 Average Rate Of Changeap Calculus

 admin



Answer

Calculus 8th Edition answers to Chapter 2 - Derivatives - 2.1 Derivatives and Rates of Change - 2.1 Exercises - Page 113 1 including work step by step written by community members like you. Textbook Authors: Stewart, James, ISBN-10:, ISBN-13: 978-1-28574-062-1, Publisher: Cengage. The average rate of change is (y2-y1)/(x2-x1). It is the same as the slope.) In this question, x1 = -1, so y1 = 2 ans x2 = 3, so y2=10. Chapter 2 Thomas Calculus solution 11th 12th 13th 14th edition solution manual Urdu Hindi The topics of discussion are Average rate of change of functions. Unit 1 – Limits and Continuity; Unit 2 – Differentiation: Definition and Fundamental Properties. 2.1 Defining Average and Instantaneous Rates. Thus the average energy of the reaction is (e 2 + 1)/ 4(e – 1) , or roughly 1.22. Mean Value Theorem for Integrals. Averages are also called means. So you may use the same formula to find the mean value of a function. There is also an important result in calculus that relates the mean value to a particular function value on the given interval.

a) $frac{f(x)-f(3)}{x-3}$ b) $f'(3) = limlimits_{h to 0}frac{f(3+h)-f(3)}{h}$

Work Step by Step

2.1 Average Rate Of Changeap Calculus Equation

2.1 average rate of changeap calculus ab

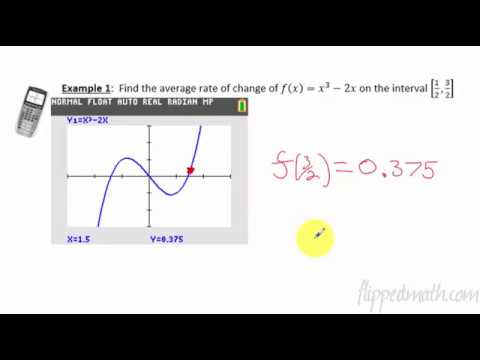
2.1 Average Rate Of Changeap Calculus Formula

For part a, we know that the secant line is the average rate of change on the interval between the two points from equation 6. To calculate the slope of this line, we need to calculate the change in y divided by the change in x: $frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}$ We can then plug our two given points into the equation to get our answer: $frac{f(x)-f(3)}{x-3}$ For part b, we know from equation 4 that the equation to find the slope of the tangent line is: $f'(x) = limlimits_{h to 0}frac{f(a+h)-f(a)}{h}$ The question tells us that point P is located at (3, f(3)). Next we can plug in 3 for a to get the equation for the tangent line: $f'(3) = limlimits_{h to 0}frac{f(3+h)-f(3)}{h}$